Minkowski Sums

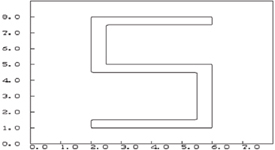
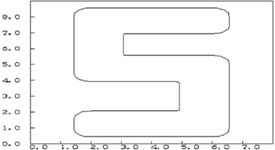
A constant-radius offset of a 2D, R-functions based set-theoretic solid, is generated by taking the Minkowski sum with a disk.

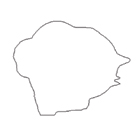
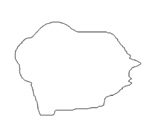
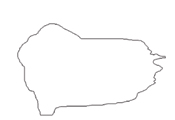
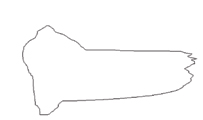
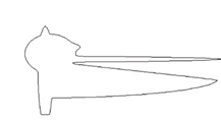
Metamorphosis of a “silly boy” into a “wise pelican” using time-weighted Minkowski sums.

Pasko A., Okunev O., Savchenko V.
Minkowski Sums of Point Sets Defined by Inequalities,
Computers and Mathematics with Applications, Elsevier Science, vol. 45, No. 10/11, 2003, pp. 1479-1487.
Electronic version: PDF (194 K)

(the first version of the paper was published in 1998 in the proceedings of the workshop Differential/Topological Techniques in Geometric Modeling and Processing, Korea)

The existing approaches support Minkowski sums for the boundary, set-theoretic and ray representations of solids. In this paper we consider the Minkowski sum operation in the context of geometric modeling using real functions. The problem is to find a real function F3(X) for the Minkowski sum of two objects defined by the inequalities F1(X) >= 0 and F2(X) >= 0 . We represent the Minkowski sum as composition of other operations: the Cartesian product, resulting in a higher dimensional object, and a mapping to the original space. The Cartesian product is realized as an intersection in the higher-dimensional space, using an R-function. The mapping projects the resulting object along N coordinate axes, where N is the dimension of the original space. We discuss the properties of the resulting function and the problems of analytic and numeric implementation, especially for the projection operation. Finally, we apply Minkowski sums to implement offsetting and metamorphosis between set-theoretic solids with curvilinear boundaries.