HyperFun: sample model

--This HyperFun program consists of one object:
--union of superellipsoid, torus and soft object

my_model(x[3], a[1])
{
array x0[9], y0[9], z0[9], d[9], center[3];
x1=x[1];
x2=x[2];
x3=x[3];

-- superellipsoid by formula
superEll = 1-(x1/0.8)^4-(x2/10)^4-(x3/0.8)^4;

-- torus by library function
center = [0, -9, 0];
torus = hfTorusY(x,center,3.5,1);

-- soft object
x0 = [2.,1.4, -1.4, -3, -3, 0, 2.5, 5., 6.5];
y0 = [8, 8, 8, 6.5, 5, 4.5, 3, 2, 1];
z0 = [0, -1.4,-1.4, 0, 3, 4, 2.5, 0, -1];
d = [2.5, 2.5, 2.5, 2.5, 2.5, 2.5, 2.5, 2.7, 3];
sum = 0.;
i = 1;

while (i<10) loop
    xt = x[1] - x0[i];
    yt = x[2] - y0[i];
    zt = x[3] - z0[i];
    r = sqrt(xt*xt+yt*yt+zt*zt);

    if (r <= d[i]) then
        r2 = r*r; r4 = r2*r2; r6 = r4*r2;
        d2 = d[i]^2; d4 = d2*d2; d6 = d4*d2;
        sum = sum + (1 - 22*r2/(9*d2) +
        17*r4/(9*d4) - 4*r6/(9*d6));
    endif;

    i = i+1;
endloop;

soft = sum - 0.2;

-- final model as set-theoretic union
my_model = superEll | torus | soft;
} 

my_model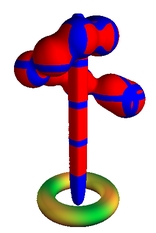 my_partition

--This object is provided as a test.

--This HyperFun program consists of one geometric object:
--union of superellipsoid, torus and soft object 

--Below two space paritions for attributes s[]
--First paritition
-- consisting in a union of blocks (5x5x5)
-- between blocks, attribute is a blue color
-- inside the block, attribute is a blue color
--Second parition
-- consisting in a torus

my_partition(x[3],a[1],s[3])
{
array xxt[3],center[3];

----------------
--first parition
 blocks = -1; --function value for the block partition
i=0;
j=0;
k=0;
dx = 3.35;  -- size of the bricks in x direction
dy = 3.35;  -- size of the bricks in y direction
dz = 3.35;  -- size of the bricks in z direction
NN = 5;     -- size of the grid of blocks: NNxNNxNN

  while (i<NN) loop     --loop along x axis
    j=0;
    while (j<NN) loop     --loop along y axis     
      k=0;
      while (k<NN) loop     --loop along z axis
        --definition of the block center
        center[1] = -10 + i*(4);
        center[2] = -6 + j*(4);         
        center[3] = -10 + k*(4); 	
        
        --union of the blocks
        blocks = blocks | hfBlock(x,center,dx,dy,dz);
        k =k+1;
      endloop;  
      j=j+1;
    endloop;
    i=i+1;
  endloop;
  --default color: mortar
  s[1] = 0.0;
  s[2] = 0.0;
  s[3] = 1.0;
  -- color of the briks
  if(blocks>=0.0) then
    s[1] = 1.0;
    s[2] = 0.0;
    s[3] = 0.0;
  endif;

----------------
--second parition
-- torus is a partition corresponding to the torus in the geometry model
-- torus is defined by library function: a bit larger than the one defined in my_object
  center = [0, -9, 0]; 
  torus = hfTorusY(x,center,3.5,1.2);

 if(torus > -0.01) then
    s[1] = hfA_Wave(x[1],0,1,1);
    s[2] = hfA_Wave(x[2],0.2,0.8,2);
    s[3] = 0.2;
  endif;
 
my_partition = blocks | torus;
}

my_model(x[3], a[1], s[3])
{
array x0[9], y0[9], z0[9], d[9], center[3];

x1=x[1];
x2=x[2];
x3=x[3];

-- superellipsoid by formula
superEll = 1-(x1/0.8)^4-(x2/10)^4-(x3/0.8)^4;

-- torus by library function
center = [0, -9, 0]; 
torus = hfTorusY(x,center,3.5,1);

-- soft object 
x0 = [2.,1.4, -1.4, -3, -3, 0, 2.5, 5., 6.5];
y0 = [8, 8, 8, 6.5, 5, 4.5, 3, 2, 1];
z0 = [0, -1.4,-1.4, 0, 3, 4, 2.5, 0, -1];
d = [2.5, 2.5, 2.5, 2.5, 2.5, 2.5, 2.5, 2.7, 3];
sum = 0.;
i = 1;
while (i<10) loop 
     xt = x[1] - x0[i]; 
     yt = x[2] - y0[i]; 
     zt = x[3] - z0[i]; 
     r = sqrt(xt*xt+yt*yt+zt*zt);
     if (r <= d[i]) then 
          r2 = r*r; r4 = r2*r2; r6 = r4*r2; 
          d2 = d[i]^2; d4 = d2*d2; d6 = d4*d2; 
          sum = sum + (1 - 22*r2/(9*d2) + 17*r4/(9*d4) - 4*r6/(9*d6)); 
     endif; 
     i = i+1; 
endloop; 
soft = sum - 0.2; 

model =  superEll | torus | soft;

--define the space partition around this model and attributes obtained in s[] array
if ( model > -0.1) then
  tmpP = my_partition(x,a,s);
endif;

-- final geometry model with attributes returned in s[] array
my_model =model ; 
}